Integrais definidas na determinação de características em estruturas metálicas na construção de um galpão
DOI:
https://doi.org/10.31533/pubvet.v18n12e1704Palavras-chave:
Arquitetura, centroide, gravidadeResumo
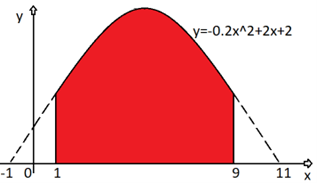
Este estudo tem como objetivo demonstrar a aplicação prática do cálculo de integrais definidas na determinação de características geométricas de estruturas metálicas, essenciais para a construção civil. Existe uma preocupação por parte de professores e coordenadores pedagógicos quanto o ensino e aprendizagem de disciplinas específicas, levando o aluno à falta de estímulo e consequentemente a evasão escolar. Para ilustrar o uso de integrais, imagine um engenheiro civil projetando um galpão agrícola. O telhado desse galpão pode ser modelado por uma função quadrática do tipo . Além disso, a estrutura sujeita a uma carga distribuída, proveniente do próprio peso e de outros elementos sobre ela. Nos casos em que a geometria se mostra ineficiente, apresentaremos o conceito de integral definida. “Sejam e dois números tais que e uma função contínua em , com para todo pertencente a esse intervalo, o teorema fundamental do cálculo diz que se for continua em um intervalo , então é contínua em certo intervalo , para qualquer temos que: é uma antiderivada de definida para todo ou seja: . À aplicação da integral na construção civil é muito variada e extremamente útil, principalmente no cálculo de estruturas metálicas utilizadas nas construções modernas, como por exemplo, para determinar o centro de massa de um corpo perfeitamente homogêneo quando submetido a campo gravitacional constante, denomina-se de área sob a curva entre e como sendo a área da região limitada pelo gráfico da função , pelas retas verticais e e pelo eixo das abscissas.
Referências
Alvarenga, K. B., & Dorr, R. C. (2017). O ensino e a aprendizagem de cálculo diferencial e integral: Características e interseções no centro-oeste brasileiro. Revista Brasileira de Ensino Superior, 2(4), 46–57. https://doi.org/10.18256/2447-3944/rebes.v2n4p46-57.
Hitt, F., & González-Martín, A. S. (2016). Generalization, covariation, functions, and calculus. In The Second Handbook of Research on the Psychology of Mathematics Education: The Journey Continues. https://doi.org/10.1007/978-94-6300-561-6_1.
Jaworski, B., Mali, A., & Petropoulou, G. (2017). Critical theorising from studies of undergraduate mathematics teaching for students’ meaning making in mathematics. International Journal of Research in Undergraduate Mathematics Education, 3(1), 168–197. https://doi.org/10.1007/s40753-016-0044-z.
Jones, S. R., & Watson, K. L. (2017). Recommendations for a “Target Understanding” of the derivative concept for first-semester calculus teaching and learning. International Journal of Research in Undergraduate Mathematics Education, 199–227. https://doi.org/10.1007/s40753-017-0057-2.
Ponce-Campuzano, J. C. (2013). Developing prospective mathematics teachers in Mexico: A lesson on the relationship between integration and differentiation. International Journal of Mathematical Education in Science and Technology, 44(7), 996–1006. https://doi.org/10.1080/0020739X.2013.826386.
Ponte, J. P., Mata-Pereira, J., Quaresma, M., & Velez, I. (2017). Formação de professores dos primeiros anos em articulação com o contexto de prática de ensino de matemática. Revista Latinoamericana de Investigacion en Matematica Educativa, 20(1), 71–94. https://doi.org/10.12802/relime.17.2013.
Racheli, J., Denardi, V. B., & Bisognin, V. (2022). Estudo da integral definida por meio de problemas interdisciplinares do cálculo com a físico-química. Revista Thema, 21(1), 274–288. https://doi.org/10.15536/thema.v21.2022.274-288.2359.
Ramos, N. S., Trevisan, A. L., & Mendes, M. T. (2019). Delineamento de tarefas de cálculo diferencial e integral envolvendo sequências numéricas: Análise de um processo. Alexandria: Revista de Educação em Ciência e Tecnologia, 12(2), 27–49. https://doi.org/10.5007/1982-5153.2019v12n2p27.
Trevisan, A. L., & Mendes, M. T. (2018). Ambientes de ensino e aprendizagem de cálculo diferencial e integral organizados a partir de episódios de resolução de tarefas: Uma proposta. Revista Brasileira de Ensino de Ciência e Tecnologia, 11(1), 209–227. https://doi.org/10.3895/rbect.v11n1.5702.
Verzosa, D., Guzon, A. F., & De las peñas, M. L. A. N. (2014). Using dynamic tools to develop an understanding of the fundamental ideas of calculus. International Journal of Mathematical Education in Science and Technology, 45(2), 190–199. https://doi.org/10.1080/0020739X.2013.790513.
Wagner, J. F. (2018). Students’ obstacles to using riemann sum interpretations of the definite integral. International Journal of Research in Undergraduate Mathematics Education, 4(3), 327–356. https://doi.org/10.1007/s40753-017-0060-7.
Downloads
Publicado
Edição
Seção
Licença
Copyright (c) 2024 Juracy Mendes Moreira, Wender Marcos Oliveira, Douglas Gomes Goncalves, Paulo Henrique do Nascimento, Elielton Olimpio da Silva Junior, Gisley de Souza Brito

Este trabalho está licenciado sob uma licença Creative Commons Attribution 4.0 International License.
Você tem o direito de:
Compartilhar — copiar e redistribuir o material em qualquer suporte ou formato
Adaptar — remixar, transformar, e criar a partir do material para qualquer fim, mesmo que comercial.
O licenciante não pode revogar estes direitos desde que você respeite os termos da licença. De acordo com os termos seguintes:
Atribuição
— Você deve dar o crédito apropriado, prover um link para a licença e indicar se mudanças foram feitas. Você deve fazê-lo em qualquer circunstância razoável, mas de nenhuma maneira que sugira que o licenciante apoia você ou o seu uso. Sem restrições adicionais
— Você não pode aplicar termos jurídicos ou medidas de caráter tecnológico que restrinjam legalmente outros de fazerem algo que a licença permita.




